七年级上册数学整式及因式分解考点

七年级上册数学整式及因式分解考点

一、代数式用运算符号把数和字母连接而成的式子叫做代数式

二、整式的相关概念

（1）单项式：由数字与字母或字母与字母的乘积所组成的代数式叫做单项式.单独一个数字或字母也是单项式

（2）多项式：几个单项式的和叫做多项式

（3）整式：单项式和多项式统称为整式 

三、整式的运算

（一）加减运算(实质是合并同类项)

1.同类项：所含字母相同，并且相同字母的指数也相同的单项式；所有的常数项都是同类项

2.合并同类项①母和字母的指数不变②系数相加减作为新的系数，如2xy²+3xy²=5xy²3.去括号法则①括号前是“+”号，去括号后，括号内各项都不变号，如a+(b+c)=a+b+c②括号前是“-”号，去括号后，括号内各项都变号，如a-(b+c)=a-b-c

（二）幂的运算(m，n为正整数)

1.同底数幂的乘法：底数不变，指数相加，a^m·aⁿ=a^m+n

2.同底数幂的除法：底数不变，指数相减，a^m÷aⁿ=a^m-n(a≠0)

3.幂的乘方：底数不变，指数相乘，(a^m)ⁿ=a^mn

4.积的乘方：把积的每一个因式分别乘方，再把所得的幂相乘，(ab)ⁿ=aⁿbⁿ

【满分技法】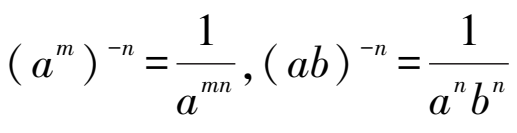
（三）乘法运算

1. 单项式乘单项式：把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式，如2a²·ab²=2a³b²

2. 单项式乘多项式：根据分配律用单项式去乘多项式的每一项，再把所得的积相加，如m(a+b+c)=ma+mb+mc

3. 多项式乘多项式：先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加，如(m+n)(a+b)=ma+mb+na+nb

4. 乘法公式①完全平方公式：(a+b)²=a²+2ab+b²(或(a-b)²=a²-2ab+b²)(a-b)²=a²-2ab+b²(或(a+b)²=a²+2ab+b²)②平方差公式：(a+b)(a-b)=a²-b²  

(四) 、因式分解

（一）定义：把一个多项式化成几个整式的积的形式

（二）基本方法

1. 提公因式法①ma+mb+mc=m(a+b+c)②公因式的确定★系数：取各项系数的最大公约数★字母：取各项相同的字母或因式★指数：取各项相同字母的最低次数

2. 公式法：①a²+2ab+b²=(a+b)²②a²-2ab+b²=(a-b)²③a²-b²=(a+b)(a-b)

（三）一般步骤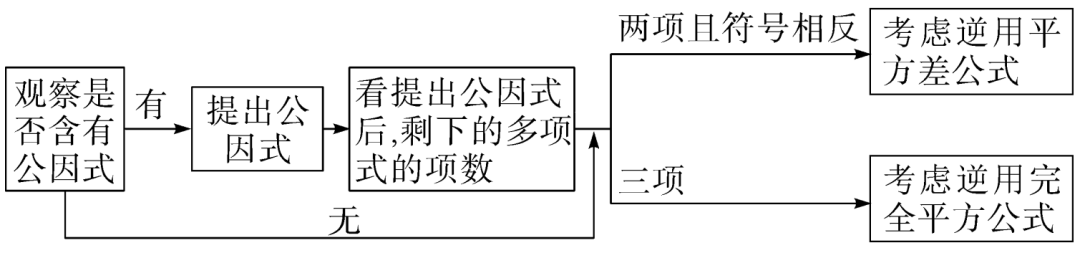

【满分技法】因式分解一定要分解到每个因式都不能再分解为止。